 Las ecuaciones existen desde hace muchos años, los egipcios desarrollaron en el siglo XVI a.c un álgebra que utilizaron para resolver los problemas cotidianos que tenían que ver con sus tierras y objetos materiales. La ciencia usa de manera regular las ecuaciones para representar leyes, las cuales son representadas por variables.
Las ecuaciones existen desde hace muchos años, los egipcios desarrollaron en el siglo XVI a.c un álgebra que utilizaron para resolver los problemas cotidianos que tenían que ver con sus tierras y objetos materiales. La ciencia usa de manera regular las ecuaciones para representar leyes, las cuales son representadas por variables.
En el principio de nuestra era un grupo de chinos matemáticos escribieron un libro llamado «los nueve capítulos sobre el arte matemático» ahí plantearon varios métodos para las soluciones de ecuaciones. uno de los primeros en utilizar símbolos en las ecuaciones fue el matemático griego Diofanto de Alejandría, quien trató las ecuaciones de primer y segundo grado.
Una ecuación es una desigual donde aparece por lo menos una variable que debe de ser descubierta. Los datos dentro de una ecuación pueden ser coeficientes, números, constantes o variables. Para que una ecuación pueda ser resuelta la variable debe de cumplir con los valores de la igualdad.
En el área de la astrología una ecuación es la diferencia que surge de la comparación del movimiento con el desplazamiento aparente o verdadero de un astro.
En química una ecuación es la representación simbólica de una reacción química. Con esto se puede determinar las cantidades de reactivos y productos utilizados en una reacción.
Clasificación de las ecuaciones según su numero de incógnita
- Algebraicas o lineal: serán algebraicas o lineal si tienen números y letras. Ejemplo: ×+8=10.
- Ecuaciones numéricas: serán ecuaciones numéricas si solo tienen números y una sola letra que en este caso representaría una incógnita. Empleo: (7+10-×)-4=6.
Tipos de ecuaciones
Ecuaciones de primer grado
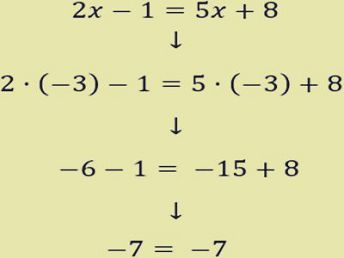 Son aquellas ecuaciones que tienen un planteamiento de igualdad donde hay una o más variables a la primera potencia. Este tipo de ecuación se resuelve solo con sumas y restas de variables expresadas a la primera potencia.
Son aquellas ecuaciones que tienen un planteamiento de igualdad donde hay una o más variables a la primera potencia. Este tipo de ecuación se resuelve solo con sumas y restas de variables expresadas a la primera potencia.
Ejemplo: 3x -2 = 16.
Ecuación de segundo grado
Son aquellas ecuaciones que tienen forma de suma algebraica donde su grado máximo es el número dos y siempre tendrán un polinomio de segundo grado.
Ejemplo: ax(2) + bx + c = 0.
Ecuación integral
 Su incógnita aparece dentro de una integral. Fueron presentadas por primera vez por un físico y matemático italiano llamado Vito Volterra. Son llamadas así, debido a la línea integral que le da función a la incógnita.
Su incógnita aparece dentro de una integral. Fueron presentadas por primera vez por un físico y matemático italiano llamado Vito Volterra. Son llamadas así, debido a la línea integral que le da función a la incógnita.
Ejemplo: v(x) x(t) v(x) = dx(t)/dt.
Ecuación funcional
Estas ecuaciones tienen mucho en común con las ecuaciones integrales, estas ecuaciones en muchos de los casos no se le puede aplicar la reducción de términos.
Ejemplo: 2 (3x – 1) – (2 + x) = 4 (x + 1).
Ecuación diofántica
Son ecuaciones que por tener distintas variables según números enteros y naturales, tendrán como resultado números enteros.
Ejemplo: a x +b y = c.
Ecuación binómica
 Estas son las ecuaciones que poseen dos términos. Estas se resuelven con la factorización o utilizando la fórmula de Abraham Moivre, este tipo de ecuación solo tiene raíces simples.
Estas son las ecuaciones que poseen dos términos. Estas se resuelven con la factorización o utilizando la fórmula de Abraham Moivre, este tipo de ecuación solo tiene raíces simples.
Ejemplo: 7 (3-x) = 5 (x + 1).
Ecuación polinómica
Son las que tienen tres términos, este tipo de ecuación también es conocida como ecuaciones trinómicas. Estas ecuaciones cuentan con un primer término que es un polinomio y el segundo es cero.
Ejemplo: 4x – 5 = 0.
Ecuación fraccionaria
Son esas ecuaciones que poseen uno o más denominadores en uno de sus términos y la variable se encuentra en el denominador. Para resolver este tipo de ecuación hay que tener en cuenta que las raíces del numerador es la solución siempre y cuando tenga sentido con la con la original.
Ejemplo: x/16 – 1/12 = 1/3.
Ecuación entera
Son esas ecuaciones donde todos sus términos son enteros.
Ejemplo: 7x + 3y – 4 = 3y – 5.
Ecuación racional
 Son las ecuaciones donde ninguno de sus términos lleva la incógnita bajo su radical. Este tipo de ecuación es una expresión racional que lleva una o varias variables en el denominador o en el denominador.
Son las ecuaciones donde ninguno de sus términos lleva la incógnita bajo su radical. Este tipo de ecuación es una expresión racional que lleva una o varias variables en el denominador o en el denominador.
Ejemplo: 2/3 – 5/6 = 1/x.
Ecuación irracional
Son las ecuaciones donde al menos uno de sus términos lleva la incógnita bajo un radical. Estas ecuaciones mediante operaciones algebraicas pueden ser reducidas a una ecuación algebraica racional.
Ecuación diferencial
Son ecuaciones que contienen partes de las variables. Esta es una de las ecuaciones más comunes, por lo tanto son usadas en diferentes disciplinas como la economía, la física, la ingeniería, la biología, etc.
Las ecuaciones diferenciales son resueltas por fórmulas explícitas, pero se pueden determinar algunas de sus propiedades de una ecuación diferencial en específico, sin encontrar su solución exacta.
Ejemplo: y´+ p(x) y = q(x) y.