 En el lenguaje común se denomina productos notables a los bienes que pueden ser conseguidos en el mercado y que poseen propiedades específicas. Algunos ejemplos de estos productos pueden ser un reloj de mucho valor, un vehículo de lujo, un ordenador de última actualización.
En el lenguaje común se denomina productos notables a los bienes que pueden ser conseguidos en el mercado y que poseen propiedades específicas. Algunos ejemplos de estos productos pueden ser un reloj de mucho valor, un vehículo de lujo, un ordenador de última actualización.
De igual forma, se definen los productos notables como aquel resultado que se consigue sin requerir la realización de una operación de multiplicación, debido a que se considera suficiente analizarse de memoria su progreso clásico.
La noción de producto, en las matemáticas, se vincula al resultado de una operación multiplicativa. Las variables que participan en dichas operaciones, son conocidas en el ámbito matemático como factores.
Asimismo, los productos notables son descritos como las multiplicaciones con representaciones algebraicas cuya operación final puede ser plasmada por simple indagación, sin comprobar la multiplicación que satisfacen diversas normas invariables.
Su ejecución facilita y organiza la solución de diversas multiplicaciones usuales. Los productos notables están vinculados a un enunciado de factorización.
Tipos de productos notables
Monomio por polinomio
En este tipo de producto notable se multiplica la variable que se encuentra solo es decir, el monomio, por cada una de las dos variables, cuatro o cinco variables, pudiendo ser un binomio, o por un polinomio.
Suma de cubos
 En el momento en que se ve el producto entre la adición de dos términos, y el primero al cuadrado menos el primero multiplicado por el segundo, sumando el segundo al cuadrado. Hay una manera muy fácil de solucionarlo, que engloba la adicionar el cubo del primer término al del segundo.
En el momento en que se ve el producto entre la adición de dos términos, y el primero al cuadrado menos el primero multiplicado por el segundo, sumando el segundo al cuadrado. Hay una manera muy fácil de solucionarlo, que engloba la adicionar el cubo del primer término al del segundo.
Monomio por monomio
En este tipo de producto, el resultado generado es otro monomio, se realiza una multiplicación de los coeficientes y se adicionan sus segmentos laterales siempre que poseen un mismo fundamento.
Binomio al cubo
En el binomio al cubo, ocurre el mismo procedimiento que en el binomio al cuadrado, es decir, se divide en adición y resta.
En el caso de la suma, se refiere del cubo de la suma de dos términos, que es semejante al cuadrado de la primera variable, más el triple de la primera al cuadrado multiplicada por la segunda, en adición se coloca el triple de la primera por la segunda al cuadrado, más la segunda variable al cubo. En el caso de la resta, se alterna el primero y el último signo.
Cuadrado del binomio
 En este tipo de producto el cuadrado de la adición de dos cantidades es equivalente al cuadrado de la primera cantidad junto con el doble de la primera cantidad por la segunda más el cuadrado de la segunda cuantía.
En este tipo de producto el cuadrado de la adición de dos cantidades es equivalente al cuadrado de la primera cantidad junto con el doble de la primera cantidad por la segunda más el cuadrado de la segunda cuantía.
Binomio suma por binomio diferencia
Consiste en el resultado entre un binomio en el que sus términos se adicionan y otro, en el que se reducen o restan. Para descifrarlo, es suficiente realizar una resta del cuadrado de cada término.
Binomio conjugado
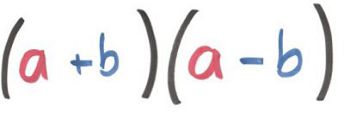 Se conocen como binomios conjugados a los productos notables que sólo se diferencian en el signo de una de las variables, dichas variables con signo distinto en cada binomio se le conoce como simétricos. El producto de dos binomios de tipo conjugado es semejante al cuadrado de la variable común, restando el cuadrado de la variable simétrica.
Se conocen como binomios conjugados a los productos notables que sólo se diferencian en el signo de una de las variables, dichas variables con signo distinto en cada binomio se le conoce como simétricos. El producto de dos binomios de tipo conjugado es semejante al cuadrado de la variable común, restando el cuadrado de la variable simétrica.
Trinomio suma al cuadrado
Para lograr esta clase de producto notable se calcula el cuadrado de la primera variable, adicionando el cuadrado de la segunda variable, más el cuadrado de la tercera variable, junto con el duplo del producto del primero multiplicado por el segundo, más el duplo del segundo multiplicado por el tercero, más el doble producto de la tercera variable multiplicada por la primera.
Usos de los productos notables
- Facilita la elaboración de una valoración de la cantidad de sujetos que se localizan en un algoritmo general.
- Se utiliza para calcular de la deformación de diferentes estructuras.
- Los productos notables se aplican para hacer cálculos de la potencia de una corriente de tipo eléctrica.